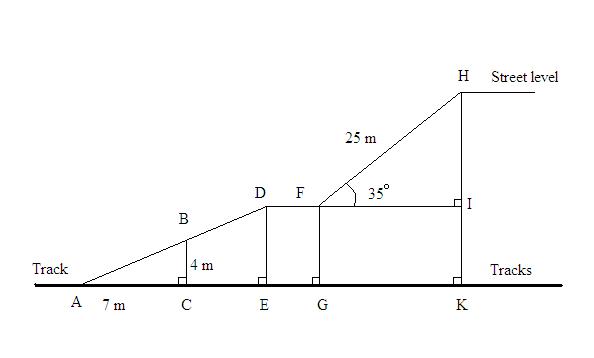
The picture shows a sketch of escaladers in the underground station in Kyoto.
The escaladers go from A that lies on the track, over D to F, and ends in H which lies in the street level. Some of the measures are already on the picture.
– Find the lengths of D to E
– Find the angel A and the length of the escalader from A to D
The escalader from F to H is 25 meters long
– Find the high differences between tracks and street level (K to H)
– Find the length from A to K

Recent Comments