Le But de l’application:
Afficher un nombre binaire correspondant au nombre décimal entré.
Moyen mis en oeuvre pour ce tutoriel:
-Utilisation des “ifelse” et “for range” dans le bloc “control” du bloc editor
-Utilisation des “Lists” (et oui encore) en plus approfondit.
-Utilisation des puissances (ex: 2^10) dans app inventor ( avec la fonction “expt”)
1) Prérequis:
Aucun ! ou presque : Beaucoup de temps devant soit et une bonne dose d’aspirine si vous n’êtes pas encore entré dans le monde de la programmation.
2) Objectif:
Avec un nombre entré par l’utilisateur (dans une hint box) calculer le nombre binaire et l’afficher dans un label ainsi que le nombre de bits qui le composent.
3) Structure dans App Inventor:
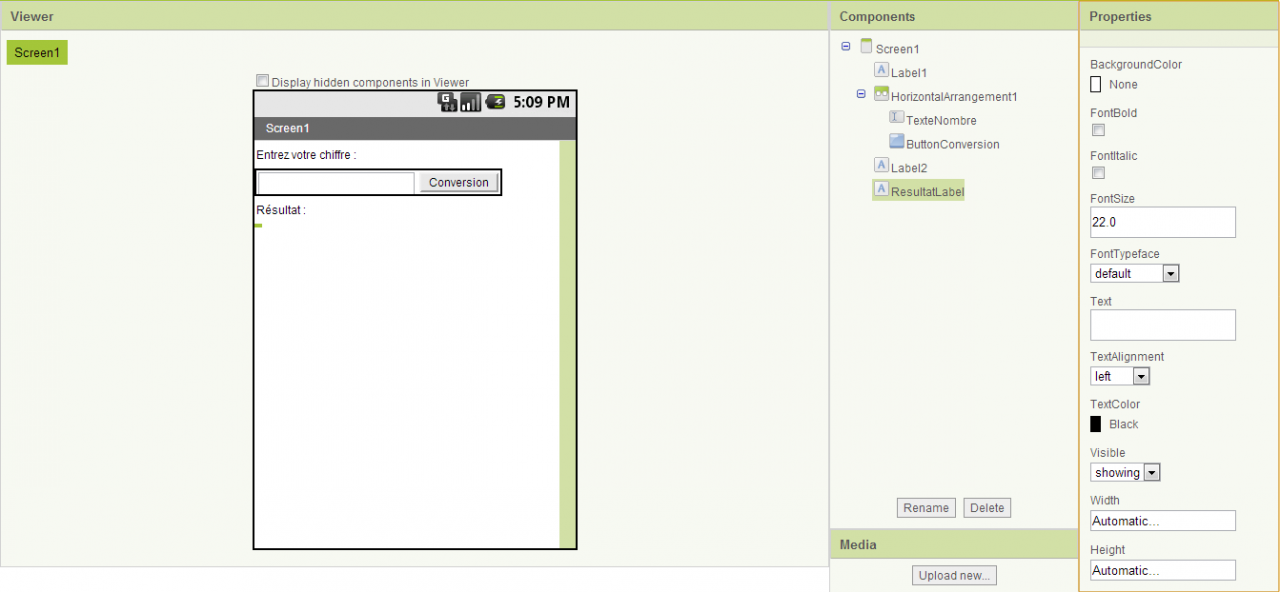
J’ai sélectionné le label prévu pour le résultat puisque je n’avait rien mis dedans
Source : Image LP2I
-1 hintbox
-1 bouton
-1 label pour le résultat
-1 label pour le nombre de bits (facultatif)(Attention le label n’est pas présent quand j’ai pris le screen de ma fenêtre app inventor)
Voilà c’était très dur je conçois, maintenant on passe à la suite :
4) Editor :
4.1 Définitions des variables et autres listes :
Variables avec… Rien dedans !:
Voila tout est dit on va donc créer 2 variables avec des text vides:
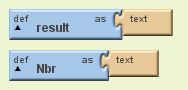
2 variables vides !
Source : Image LP2I
Nbr: récupère le nombre rentré dans le hintbox pour lui faire subir toutes les opérations que l’on veut.
result: stocke le nombre binaire final
On crée une variable Bits qui va stocker les 16 bits dont on a besoin. On va donc créer une liste avec 16 zéros :
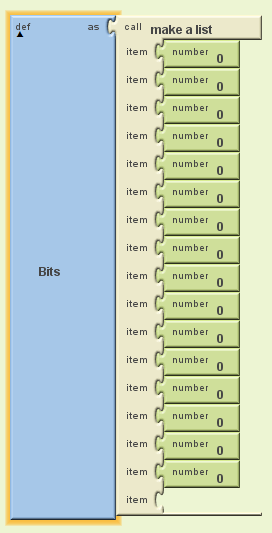
Voila une belle liste de zéros
Source : Image LP2I
4.2 Une fonction = tout le programme
Et oui le programme n’a qu’un seul évènement : l’appui sur le bouton conversion.
On va donc ajouter à notre bloc editor une seule et unique fonction “ButtonConversion.Click”
Source : LP2I
On va ensuite initialiser nos fonctions pour les remettre à zéros (si l’on veut faire plusieurs conversions) et assigner le nombre rentré par l’utilisateur dans la variable Nbr.
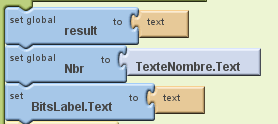
A chaque fois que l’on appuie sur le bouton Conversion. Les variables result et BitsLabel sont mis à zéro, Nbr prend la valeur du nombre entré par l’utilisateur.
Source : LP2I
Mise en place des “ifesles”:
C’est la que ça ce corse
On à 3 type de longueur de bits : 4, 8 et 16
On a donc trois ifelses comme ceci:
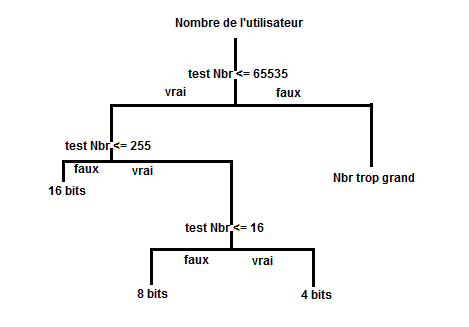
Un petit schéma pour que ce soit clair ^^
Source : LP2I
Les tests sont logiques puisque le nombre maximum pour:
-16 bits = 65535
-8 bits = 255
-4 bits = 16
Voilà la structure dans app inventor :
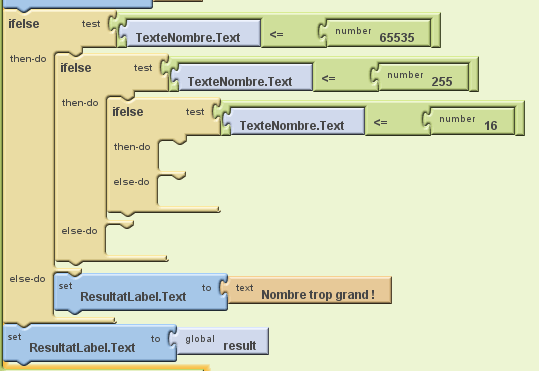
Voila la structure dans app inventor (j’ai pris aussi la fin de la fonction avec “set ResultatLabel to result”)
Source : LP2I
Gardez bien à l’esprit le schéma de tout-à-l’heure puisqu’il va nous guider pour la suite.
Programme de conversion 16 bits
Voila la procédure de conversion pour 16 bits elle est relativement similaire aux autres (8 et 4) je ne develloppe donc que celle-ci.
On sait que pour convertir un nombre décimal il faut le soustraire au différentes puissances de 2. Si la soustraction est possible le bits correspondant à la puissance (2^2 = bit 3) prend la valeur 1, on effectue la soustraction et on passe au bit suivant. Si elle n’est pas possible on passe directement à la puissance suivante soit le bit suivant (le bit que l’on a passé prend alors la valeur 0).
Cette procédure doit se répéter le nombre de fois qu’il y a un bit (soit 16 fois ici) on ne va donc pas la modélisée 16 fois (je vois vos yeux qui brillent) et on va plutôt utiliser une boucle.
La boucle “for range”
D’abord c’est quoi une boucle ?
C’est une fonction très pratique de la programmation qui nous permet de répéter un nombre de fois défini (ou infini) une même action.
Maintenant que c’est clair pour tout le monde je continue :
On veut que la boucle ce répète un nombre de fois défini (le nombre de fois qu’il y a de bits je rappelle)
Donc notre boucle aura 16 cycle ici
Ensuite, on veut que à chaque fois qu’un cycle s’exécute :
-On teste le nombre avec une première puissance de 2 (la première pour 16 bits c’est 2^15).
-Si on peut le soustraire on soustrait la puissance à notre nombre et on change le bit correspondant par la valeur 1.
-Si on ne peut pas le soustraire on ne fait rien et on change le bit correspondant par la valeur 0.
Dit comme ça c’est simple maintenant dans le bloc editor :
Essayer de placer tout seul la boucle “for range” qui se trouve dans la palette “built-in”/”control” (ref. au schéma plus haut. Rappel : c’est la procédure 16 bits)
Une fois placée vous devez obtenir ceci :
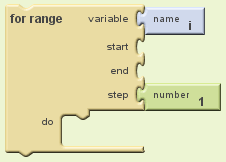
Voilà la boucle de base crée par App inventor
Source : Image LP2I
-variable i: (vous pouvez la renommer) elle fait partie de la boucle for (elle ne peut pas être utilisée ailleurs) et représente le numéro de cycle.
-start: il faut mettre un nombre ici qui représente le départ de la boucle (j’ai mis zéro dans mon cas)
-end : idem sauf que c’est l’arrivée (j’ai mis 15. De 0 à 15 il y a 16 cycles, pile ce qu’il nous faut)
-step : tout simplement le pas entre 2 cycles (ici quand la boucle se répète on ajoute à la variable i 1. Laissez comme tel)
ce qui doit donner ça :
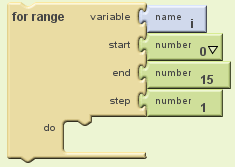
Voila on a fait le plus facile (ne faites pas cette tête la j’ai pas eu la correction moi)
Source : LP2I
Ne reste plus qu’a la remplir attaquons dès maintenant le plus difficile :
Dans la procédure j’ai dit “si” il y a donc un “ifesle” dans la boucle.
Son test par contre est différent des autres parce que l’on veut savoir si une soustraction est possible ou pas.
C’est la qu’il va falloir ruser parce qu’on ne peut tester qu’une égalité ou une inégalité.
Quand on fait la soustraction d’un nombre plus grand sur un nombre plus petit (quand la puissance est trop grande par rapport au nombre)
le nombre devient… négatif !
se qui nous donne :
(l’opération de la puissance sur le nombre) >= 0.
On teste donc si le nombre est supérieur ou égal à 0.
L’opération de la puissance sur le nombre :
Dans la procédure on veut soustraire le nombre à la puissance correspondant au bit voulu.
On place donc le nombre soustrait par la puissance.
la puissance :
Plus compliqué ici puisqu’on va devoir récupérer notre variable i pour celle-ci. En effet si on veut que la puissance change quand un cycle change il faut donc introduire la variable de celui-ci.
Il faut aussi savoir comment on introduit une puissance dans app inventor.
Voilà magie :

Ici la variable i est X
Source : Image LP2I
-On retrouve donc le … >= 0
-On soustrait le chiffre (Nbr)…
-… a 2^15-X ici
Pourquoi 15-X ? puisque la variable commence à 0 et que nous on veut commencer par la dernière puissance (2^15).
Donc à chaque cycle de la boucle “for” la puissance va diminuer.
La conversion :
On va se placer dans le cas ou la condition est vrai (on fait prendre la valeur 1 au bit)
Il faut d’abord que l’on enlève la valeur de la puissance et que l’on stocke le résultat dans la variable Nbr pour pouvoir utiliser le nombre sur la puissance inférieure dans la prochaine boucle.

ça ne vous rappelle rien ?
Source : Image LP2I
Et oui c’est la même chose qu’au dessus sauf que ce n’est plus un test.
Ensuite, on va remplacer un item de la liste bits.
Pour cela on va utiliser la fonction “replace list item”:
-On va lui indiquer la liste bits
-On va lui dire que l’index désiré c’est X+1 (normal, un index ne peut pointer vers 0 et notre boucle commence à 0)
-Et enfin on va lui dire qu’on remplace le 0 par un 1
le tout en image…

On attribue la valeur 1 au bit X+1
Source : LP2I
On rempli maintenant la partie “esledo” du “ifelse”
Ce n’est pas bien compliqué il faut juste copier le “replace list item” et changer le 1 par 0 C’est tout ^^.
Voici la fonction en entier “ifelse” dans la boucle “for”:
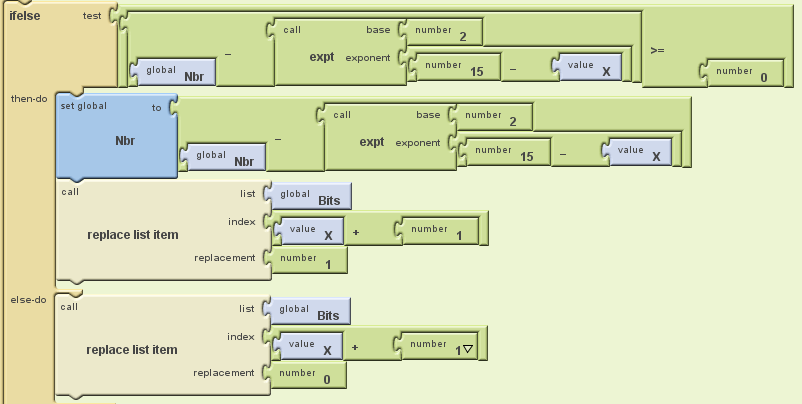
Source : Image LP2I
Attention on a pas fini la procédure 16 bits (on reste donc dans la boucle “for”) !
Il faut maintenant rassembler tout les 0 et les 1 qui composent le nombre binaire.
Pour cela on va appeler la fonction “set global result to”.
On va mettre dedans un “join” qui va rassembler à chaque fois qu’une boucle ce termine les 0 et les 1.
Il est composé d’un “select list item” qui va chercher dans la liste bits l’item 16-X (On part du plus grand bit au plus petit) et on lui ajoute le reste du nombre binaire dans la 2ème partie du “join”.

La fin de la boucle for pour 16bits.
Source : Image LP2I
Et voila vous pouvez souffler (un peu c’est pas fini mais vous avez fait le plus dur).
La boucle “for” en entier pour pas vous tromper:
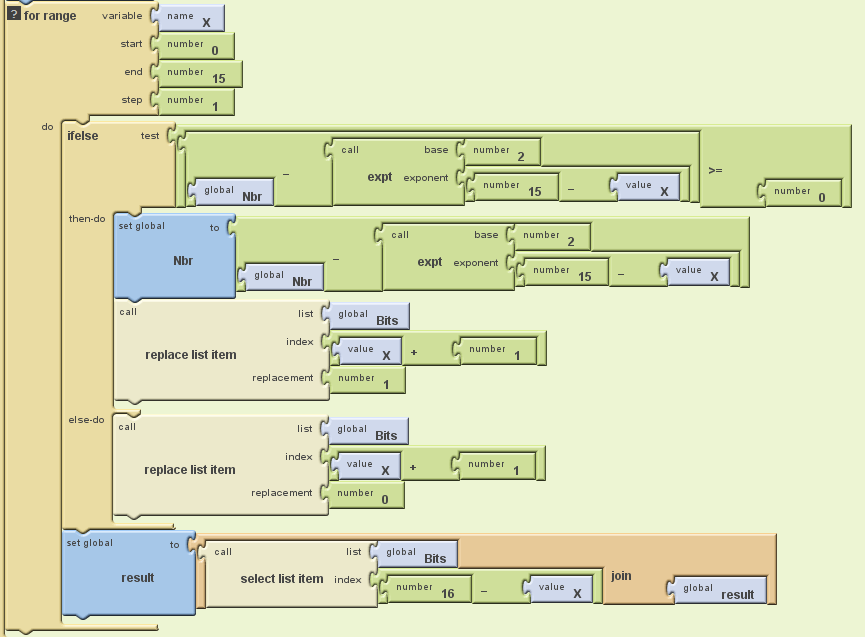
Et voilà la partie la plus dur du tuto est faite (ne vous inquiéter pas il y en a deux autres similaires ^^)
Source : LP2I
Voila vous n’avez plus qu’a refaire la même chose pour les nombres de 4 bits et 16 bits.
Je met le code source pour les feignants (ou pour la correction):
Binaire