Exercice 1.6 :
 Monsieur K.C Sakès s’est tué dans un accident de voiture en
Monsieur K.C Sakès s’est tué dans un accident de voiture en  Australie. Avant son accident, il avait expédié par bateau, une caisse à son neveu Jonathan habitant à La Rochelle. Comble de malheur, pendant le voyage, un incendie s’est déclaré à bord. Des documents ont été endommagés. Les références des caisses correspondant aux destinataires ont été partiellement brulées. Jonathan Sakès aimerait retrouver le colis expédié par son oncle.
Australie. Avant son accident, il avait expédié par bateau, une caisse à son neveu Jonathan habitant à La Rochelle. Comble de malheur, pendant le voyage, un incendie s’est déclaré à bord. Des documents ont été endommagés. Les références des caisses correspondant aux destinataires ont été partiellement brulées. Jonathan Sakès aimerait retrouver le colis expédié par son oncle.
 La seule manière de retrouver sa caisse est de déterminer ses dimensions. Voici la partie du document qui intéresse Jonathan. Sur le document, étaient indiqués :
La seule manière de retrouver sa caisse est de déterminer ses dimensions. Voici la partie du document qui intéresse Jonathan. Sur le document, étaient indiqués :
Dans la 1ère colonne les noms et prénoms des destinataires. Dans la 2nde colonne le volume en litres(??3). Dans la 3ème colonne la somme A des longueur, largeur et hauteur en (??). Dans la 4ème colonne, le numéro de la caisse inscrit sur une face.
Les dimensions sont des nombres entiers de décimètres. Avec le peu de données qu’il y a sur le document incomplet, il se rend vite compte qu’il ne peut trouver les dimensions de sa caisse. C’est alors qu’il se souvint de la lettre envoyée par son oncle et qu’il avait déjà reçue. Son oncle y faisait une remarque : la somme A correspondait à l’âge du fils de Jonathan, ce qui l’amusait. Après quelques minutes de réflexions, il se rendit compte que là encore, il ne pouvait trouver les dimensions du colis tant désiré. Il reprit la lettre et essaya d’y trouver un indice qui puisse encore l’aider. Un extrait qui lui semblait d’apparence anodin, attira quand même son attention :
« J’ai vu un docker placer la caisse verticalement, le côté le plus long vers le haut, elle était ainsi bien calée… ».
« Ah, enfin, j’ai trouvé les dimensions ! » s’exclama Jonathan Sakès.
A votre tour, déterminer les dimensions de la caisse et l’âge du fils de Jonathan.
 La courbe ci-dessous représente la coupe d’un relief de collines. On a modélisé ce relief par une fonction polynomiale du 3ème degré. L’altitude de départ est de 300 mètres. La vallée V est située à 10 kilomètres de l’axe vertical de départ et à une altitude de 360 mètres, le sommet S lui, est à 50 kilomètres de l’axe vertical de départ.
La courbe ci-dessous représente la coupe d’un relief de collines. On a modélisé ce relief par une fonction polynomiale du 3ème degré. L’altitude de départ est de 300 mètres. La vallée V est située à 10 kilomètres de l’axe vertical de départ et à une altitude de 360 mètres, le sommet S lui, est à 50 kilomètres de l’axe vertical de départ.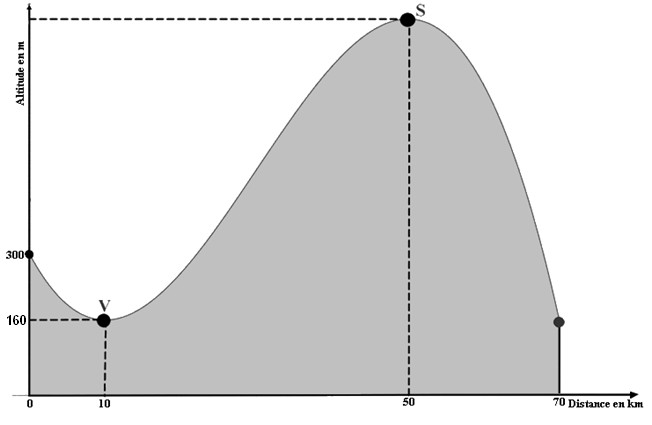
 Sur une voie ferrée rectiligne, se trouvent les gares de quatre bourgs :
Sur une voie ferrée rectiligne, se trouvent les gares de quatre bourgs :
 Le docteur Enrico Vidisenoeuf est très inquiet car le test pour détecter les malades du célèbre virus Tique ne fonctionne pas bien. Sur la population de la ville de Malchance, il a établi que :
Le docteur Enrico Vidisenoeuf est très inquiet car le test pour détecter les malades du célèbre virus Tique ne fonctionne pas bien. Sur la population de la ville de Malchance, il a établi que : L’archéologue, le Docteur Jean Déchifrepamal a découvert un site où sur un mur se trouvaient les pictogrammes ci-dessous.
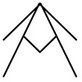
L’archéologue, le Docteur Jean Déchifrepamal a découvert un site où sur un mur se trouvaient les pictogrammes ci-dessous.





 s
s Australie. Avant son accident, il avait expédié par bateau, une caisse à son neveu Jonathan habitant à La Rochelle. Comble de malheur, pendant le voyage, un incendie s’est déclaré à bord. Des documents ont été endommagés. Les références des caisses correspondant aux destinataires ont été partiellement brulées. Jonathan Sakès aimerait retrouver le colis expédié par son oncle.
Australie. Avant son accident, il avait expédié par bateau, une caisse à son neveu Jonathan habitant à La Rochelle. Comble de malheur, pendant le voyage, un incendie s’est déclaré à bord. Des documents ont été endommagés. Les références des caisses correspondant aux destinataires ont été partiellement brulées. Jonathan Sakès aimerait retrouver le colis expédié par son oncle. La seule manière de retrouver sa caisse est de déterminer ses dimensions. Voici la partie du document qui intéresse Jonathan. Sur le document, étaient indiqués :
La seule manière de retrouver sa caisse est de déterminer ses dimensions. Voici la partie du document qui intéresse Jonathan. Sur le document, étaient indiqués :