Accueil Archive par catégorie "Ressources"

Category: Ressources

Sitographie

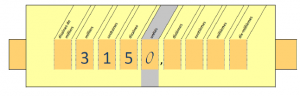
Voici des ressources proposées par Jean-Louis Durpaire, IGEN honoraire.
Calcul@tice
 
Classe TICE
 
Des outils pour la classe 
 
Geoplans
 
GoMath 
 
Haïti Futur
 
Khan academy en français
 
L’académie en ligne (CNED)

La mallette de l’Ifé
http://educmath.ens-lyon.fr/Educmath/recherche/equipes-associees/mallette 

 La monnaie au CE1
http://planete.sankore.org/xwiki/bin/view/Coll_jtesse/LamonnaieCE1

 L’attrape-nombres

L’école pour tous
http://www.ecolepourtous.education.fr/pour-enseigner.html

Les capsules de Brigitte
 
Les champions des maths
 
Les Fondamentaux (mathématiques)
 
Les réglettes Cuisenaire
 

Le site de Jean-Louis Sigrist
http://jlsigrist.com

Le Matou Matheux
 
Les cahiers Sésamath
 
Logiciel éducatif
 
Magic ten
 
Mathématiques faciles
 
Mathématiques magiques
 
Mathador
 
Math en poche
 
Maths libres
 
Millemaths
 
NRich Enriching mathematics
 

Pass Education
http://www.pass-education.fr 

Planète Sankoré
 
Primaths
 
Ressources informatiques pour l’enseignant
 
Robopacker (jeu de géométrie)
 
Si c’est pas malheureux
 
 
Ressources pour la formation
 
Arithmétique et compréhension à l’école
 
Le café pédagogique (Dossier Réinventer l’école avec le numérique)
 
Classe inversée
 
Enseigner la numération décimale
 
Géométrie (Besançon)
 
Les maths en classe (cycle 2). Un travail d’équipe avec Stella Baruk
 
Math en video
 
Math Learning Center
 
Mathome
 
Micmaths
 
Mon cerveau à l’école
 
Prim TICE
 
Séminaire « L’enseignement des mathématiques à l’école primaire »
 
 
 
Bibliographie (proposée par Jean-Louis Durpaire, IGEN honoraire)
 
Amadieu Franck. Tricot André. Apprendre avec le numérique. Retz. 2014
 
Bolsius Christophe. Fort en calcul mental ! CRDP Lorraine. 2008
 
Bonnet Nicole. La proportionnalité sans problème. SCEREN. CRDP de Franche-Comté. 2011
 
Boule François. Jeux et compétences en mathématiques au quotidien. CNDP. 2012
 
Boule François, Le calcul mental au quotidien, CRDP Dijon. 2012.
 
Brissiaud Rémy. Apprendre à calculer à l’école. Retz. 2013
 
Brissiaud Rémy. Premiers pas vers les maths. Retz. 2007
 
Brunet Alain. Durpaire Jean-Louis (sous la direction de). Le plan Ecole numérique rurale. Rapport des inspections générales. 2011 
 
Butlen  Denis. Le calcul mental entre sens et technique.  Presses universitaires de Franche-Comté, 2007
 
Calmelet Jean-Jacques (coordonné par). Situations multiplicatives. CRDP Lille. 2011
 
COPIRELEM. Calcul mental à l’école primaire – Ressources et formation. 2012
 
Davidenkof Emmanuel. Le tsunami numérique. Stock.  2014 
 
Dehaene Stanislas. La Bosse des maths: Quinze ans après. Odile Jacob. 2010 
 
Durpaire François. Mabilon-Bonfils Béatrice. La fin de l’école. PUF. 2014
 
Durpaire Jean-Louis, Bouysse Viviane, Hébrard Jean et al. L’enseignement des mathématiques au cycle 3. Rapport de l’inspection générale de l’éducation nationale. 2006
 
Durpaire Jean-Louis. Mégard Marie (Sous la direction de). Le nombre au cycle 2. Ressources pour faire la classe. CNDP. 2010. 
 
Durpaire Jean-Louis. Mégard Marie (Sous la direction de). Le nombre au cycle 3. Ressources pour faire la classe. CNDP. 2012.
 
Jouglet Marie. Morand Hélène. Grandeurs et mesures. CNDP. 2014
 
Emprin Fabien. Emprin – Charotte Fabienne. Un rallye mathématique en maternelle ? Oui, c’est possible. CRDP Champagne-Ardenne. 2009. 
 
Fayol Michel. L’Acquisition du nombre, PUF, collection « Que sais-je? », 2012
 
Gosset Hélène. Taveau Catherine. Activités géométriques autour des solides. CRDP Paris. 2010
 
Graff Olivier. Valzan Antonio. Wozniak Benoît. Jacquart André (coordonné par). Problèmes additifs et soustractifs CP-CE1. CRDP Nord-Pas-de-Calais. 2009
 
Graff Olivier. Wozniak Benoît. Calmelet Jean-Jacques (coordonné par). Situations multiplicatives. CRDP Nord-Pas-de-Calais. 2011
 
Graff Olivier. Kirch Anthony. Wozniak Benoît. Volckcrick Michel (coordonné par). Fractions et nombres décimaux. CRDP Nord-Pas-de-Calais. 2013.
 
Marie-Lise Peltier (Sous la direction de). D. Butlen, P. Masselot, B. Ngono, M. Pézard, A. Robert, D. Vergnes. Dur, dur d’enseigner en ZEP. La Pensée sauvage. 2004.
 
Villani Cedric. Théorème vivant. Le Livre de Poche. 2014

Les évaluations en 6ème, qu’en faire ?

La circulaire de rentrée ainsi que la feuille de route 100% de réussite de notre académie nous rappellent l’importance que nous devons accorder aux évaluations nationales, à leur analyse, leur traitement, dans un souci d’amélioration des résultats des élèves de notre département.
Dans ce cadre, le GAM 16, groupe d’accompagnement pour les mathématiques de Charente, a produit un outil pour faciliter l’accès aux ressources en lien avec les évaluations nationales de 6ème.

view.genial.ly/…/interactive-content-evaluations-6eme-quen-faire

Cette ressource destinée aux professeurs de cycle 3 du CM1 à la 6ème sera aussi utile pour la liaison école-collège, pour programmer et pour accompagner les élèves.

En effet, deux parcours sont proposés selon votre niveau d’enseignement afin d’accompagner au mieux les élèves en amont ou en aval des évaluations.
Vous y trouverez les préconisations de la note du 10/01/23, les fiches d’accompagnement, des propositions de programmation et des ressources locales pour mettre en œuvre un accompagnement adapté.

 

Points du vigilance sur l’utilisation du glisse-nombre aux cycles 2 et 3

On sait aujourd’hui qu’il est déconseillé de dire « quand je multiplie par 10, je pose un zéro à la fin du nombre ». En effet, cette règle permet d’obtenir le bon résultat pour les nombres entiers même pour les élèves n’ayant rien compris. c’est alors une fausse-réussite.

De plus, cette règle ne fonctionne plus lors de l’introduction des nombres décimaux.

L’erreur courante 4,5 X 10 = 4,50 résulte souvent de la règle précédente instituée au cycle 2.

Le glisse-nombre est alors un outil qui peut être intéressant pour multiplier ou diviser par 10, 100, 1000 s’il est accompagné d’une bonne verbalisation.

Exemple de bonnes verbalisations :

  • Quand je multiplie un nombre par 10, le nombre devient 10 fois plus grand.
  • Quand je multiplie un nombre par 10, chaque chiffre du nombre prend une valeur dix fois plus grande.

Exemple de mauvaise verbalisation :

  • Quand je multiplie un nombre par dix, je tire la languette vers la gauche d’une case.

En effet, ici, on donne à l’élève une astuce ou une recette qui permet d’obtenir la bonne réponse mais qui ne permet pas de mettre du sens. Cela peut déboucher encore sur une fausse-réussite.

Pour en savoir plus, les ressources EDUSCOL présentent de façon complète le glisse-nombre aux cycles 2 et 3 au travers d’exemples d’activités permettant aux élèves de construire des représentations mentales numériques et de travailler les entiers au cycle 2 et les décimaux au cycle 3.

Les documents suivants permettent de fabriquer un glisse-nombre :

Outils pour enseigner les mathématiques du cycle 1 au cycle 3

Ce document de synthèse rassemble les outils nécessaires pour concevoir et organiser l’enseignement des mathématiques du cycle 1 au cycle 3. Vous pourrez y télécharger les textes officiels et des ressources telles que les guides ou les outils d’analyse des évaluations nationales. Vous pourrez également accéder aux sites partenaires tels que le GAM16 ou l’atelier Canopé16.

 

https://ww2.ac-poitiers.fr/dsden16-pedagogie/spip.php?article1516