Je vais essayer de vous raconter mes mathématiques.

Ce ne sera pas un cours parfaitement rigoureux, il y a d’autres sites et des livres qui font cela très bien, mais une certaine façon de voir les choses et d’en parler.

Il y a beaucoup à dire, alors ce sera un peu long,

cependant voici où j’en suis pour l’instant :

une petite mathematique

Le coloriage est à la mode, cependant on peut aussi créer ses propres mandalas avec une règle et un bon compas . . .

Voici un tableau synoptique des programmes de mathématiques à l’école primaire puis au collège et en lycée qui permet une certaine vision de la continuité de la démarche d’enseignement.

Il comporte des liens vers le site d’aide du CNED (centre national d’enseignement à distance).

 synoptique programmes maths

Utiliser les moyens offerts par internet dans le cadre des enseignements me semble un impératif.
Cette adaptation nécessite des coups d’essais, des tâtonnements, des évolutions guidés entre autres par l’expérimentation.
Donc expériences …
Ce faisant survient une anecdote qui aide à réfléchir : par étourderie, je dépose sur la toile un devoir d’élève avant d’avoir ramassé tous les devoirs de la classe ; la tentation est grande pour certains de recopier.
Et internet, quand on sait s’y promener, regorge de corrections d’exercices. Il n’y a pas de raison de faire comme si elles n’existaient pas.
Une question est de savoir ce que nous en faisons. Si après avoir lu ou même copier/coller, l’élève réfléchi au contenu au point d’être capable de savoir faire un exercice semblable, c’est bien là ce que nous lui demandons. Reste ensuite à vérifier.

Mais la question la plus intéressante est celle que l’on se pose du point de vue du plagié.
Je me l’étais posé pour moi-même quand j’ai commencé à rendre mes travaux disponibles, sur intranet d’abord, puis sur internet.
Je me réponds que celui qui me copie ne me prive de rien !
Une partie non négligeable des personnes présentes sur internet considère que c’est un lieu de partage où chacun peut mettre librement à disposition des autres le fruit de son travail, on parle d’espace collaboratif.

Et lorsque c’est moi qui emprunte des travaux sur le net, je dois me poser la question du respect des droits d’auteur, du respect de l’auteur.
Il y a là un sujet dont nous allons pouvoir débattre en classe – qu’il s’agisse d’un devoir de maths ou bien d’une photo sur Facebook.

La notion de proportionnalité est facile à enseigner, difficile à assimiler pour les élèves.

Sa transmission qui commence même avant la sixième se poursuit jusqu’en terminale et dans mon expérience de lycée, il y a le souvenir que, en classe de terminale littéraire, la moitié des élèves n’ont pas intégrés la notion, de même qu’en terminale économique et sociale, il y a toujours cinq ou six élèves sur 35 qui ne savent pas manipuler des pourcentages.
En cinquième – quatrième, les élèves qui utilisent le produit en croix l’appliquent comme une recette de cuisine qui leur permet de compléter des tableaux de proportionnalité mais sans en comprendre le sens, avec pour conséquence qu’ils échouent dès que le problème posé n’est pas basique.
Il faut par ailleurs remarquer que l’on s’aperçoit, en faisant de la formation pour adultes, que la notion de proportionnalité devient évidente au fil des ans, y compris pour les adultes ayant stoppés très tôt leur formation initiale.

Si la notion est difficile, c’est que son usage est protéiforme. Si la notion est importante, c’est que ses prolongements, en dehors des usages immédiats de la vie courante sont nombreux. Par exemple, en géométrie, le théorème de Thalès qui pose tant de problèmes aux élèves de quatrième – troisième, exploite simplement la proportionnalité des côtés de triangles semblables.

Question : 3 kg de fruits coûtent 15 euros, 4 kg de fruits coûtent 20 euros, combien coûtent 7 kg de fruits ?

Au collège, changer l’ordre de certaines opérations comme je le fais dans les trois paragraphes ci-dessous est loin d’être immédiat.

Le coefficient de proportionnalité :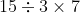
Le résultat de 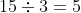 exprime concrètement ici le prix unitaire, le prix au kilo. Il permet de répondre à la question posée mais aussi à de nombreuses autres qui pourraient suivre.
Dans leur utilisation de base, les lignes trigonométriques (cosinus, sinus, tangente) sont les coefficients de proportionnalité entre les côtés de triangles pour un angle donné.
S’il convient, plutôt que de se servir du produit en croix, de mettre en avant le coefficient de proportionnalité, c’est bien en raison de son importance future : préparant l’introduction des fonctions linéaires, il débouche ensuite sur la notion de nombre dérivé qui est fondatrice de la branche des mathématiques nommée analyse, et qu’il sera indispensable de comprendre au lycée.

Le produit en colonnes :
Pour passer du prix de 3 kg au prix de 7 kg, il suffit de multiplier par  (on pourra recourir à la règle de trois). Les opérations intervenant ici sont du même ordre de celles que l’on fait en utilisant le coefficient de proportionnalité mais l’interprétation concrète du nombre 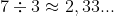 est beaucoup moins facile à exprimer. On voit ainsi que changer le sens du raisonnement dans un tableau de proportionnalité est loin d’être anodin.

Le produit en croix :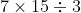
Bien sûr, si je calcule 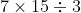 , je trouve la bonne réponse à la seule question posée, mais, puisque les élèves font les opérations les unes après les autres, une fois que l’on a calculé  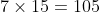, il est impossible de donner une interprétation concrète de ce nombre.
Par ailleurs, la démonstration de cette propriété à partir de la définition de la proportionnalité n’est pas très simple à comprendre :

Définition : il y a proportionnalité si et seulement si  .

-) je peux multiplier chaque membre de l’égalité par pour obtenir 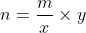 (j’utilise le coefficient de proportionnalité),
-) je peux exploiter ma compréhension des fractions (2 fractions sont égales si l’on passe de l’une à l’autre en multipliant numérateur et dénominateur par un même nombre), j’écris 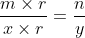 puis, ayant trouvé  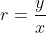, je calcule  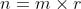 (j’utilise le produit en colonnes),
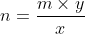-) je peux multiplier chaque membre de l’égalité dans la définition par le produit  pour obtenir, après simplification,  puis diviser chaque membre par pour avoir  (j’utilise le produit en croix).

La somme (parfois la différence) des colonnes :
Obtenir le prix de 7 kg en ajoutant les prix de 3 et 4 kg repose sur l’exploitation de la distributivité de la multiplication par rapport à l’addition . L’utilisation, hors d’un contexte simple et concret, de cette propriété, nécessite d’avoir pleinement intégré le sens profond des opérations. Il faut bien constater que cela reste difficile pour les élèves jusqu’en troisième : même s’ils acceptent les preuves évidentes de cette propriété qui leur sont fournies pendant 3 ans, le mécanisme de développement – factorisation nécessite une construction mentale qui n’est pas simple.

Tout ceci étant dit, il reste bien évident que, quand une question est posée à un élève, l’objectif est d’abord qu’il sache y répondre – peu importe les moyens -, il appartient ensuite à l’enseignant de faire évoluer les situations pour amener l’élève à adapter ses méthodes.
Donc, en clair, faites le produit en croix si vous le souhaitez, mais au tableau je ne donne pas immédiatement des explications qui l’utilise.

Des difficultés en Cinquième.

Pour une poignée d’élèves dans chaque classe de cinquième, je l’ai constaté encore la semaine dernière dans 3 classes, le raisonnement suivant n’est pas forcément choquant : (avec le précédent exemple des fruits)

« pour passer de 3 à 7, il faut ajouter 4, donc je fais 15 + 4 = 19 »

Il y a lieu de s’interroger sur la difficulté conceptuelle rencontrée ici lors du cours de mathématiques par ces enfants qui par ailleurs raisonnent tout à fait correctement.
Nul doute qu’ils connaissent parfaitement les tables de multiplication, celle de 5 notamment, et pourraient la réciter de 3 fois 5 font 15 à 7 fois 5 font 35.
Je suis enclin à penser que c’est l’intervention sous-jacente de la division qui pose problème car, bien entendu ces élèves savent calculer le prix de 7 kg si je leur donne le prix de 1 kg.
Je ne parle pas de la technique opératoire de la division (de son algorithme), mais de son sens profond : le quotient de la division du nombre a par le nombre b est le nombre q tel que le produit de q par le nombre b donne le nombre a.
Il se passe la même chose qu’avec la soustraction, une partie des élèves, bien qu’ils sachent techniquement effectuer ces opérations et parfois y recourir dans les cas standards, n’en maîtrise pas suffisamment le sens pour en exploiter le potentiel au mieux possible.

Il se peut aussi que les erreurs viennent de la difficulté à considérer le lien réciproque entre deux grandeurs, la construction abstraite que cela nécessite n’est pas immédiate.
Et à plus forte raison quand les grandeurs qui interviennent sont moins palpables. Très peu d’élèves sont capables de réussir le même exercice quand la forme en est modifiée :
« Il me faut 3 secondes pour télécharger 15 mégaoctets, combien de temps me faut-il pour télécharger 35 mégaoctets ? »

Enfin naturellement, un autre obstacle est de parvenir à automatiser le processus réfléchi pour l’appliquer aussi avec des nombres moins visualisables :
« En 2009, la production française d’énergie nucléaire s’élevait à 390 terawattheure. Le rendement d’une installation photovoltaïque est estimé à 160 kWh/an/m2. Calculer la surface qu’il faudrait recouvrir pour remplacer les centrales nucléaires. »
(il s’agit bien là d’un exercice sur la proportionnalité, notre objectif est de savoir le traiter en quatrième).

Et encore, je n’ai pas mis de nombres à virgules !

Vaste sujet dont nous reparlerons un jour . . .

En troisième, lors d’un chapitre sur les nombres, nous étudions l’algorithme des différences et l’algorithme d’Euclide.
Pour certains élèves, il peut sembler inutile d’apprendre à trouver un résultat en une succession d’étapes éventuellement laborieuses, alors que la calculatrice fournit directement ce résultat.
Il est nécessaire de comprendre que cette démarche a pour but de les initier à une branche des mathématiques dont l’importance s’accroît régulièrement au fur et à mesure de l’envahissement de notre quotidien par les systèmes informatiques.

L’algorithmique est l’ensemble des règles et des techniques qui sont impliquées dans la  définition et la conception d’algorithmes, c’est-à-dire de processus systématiques de résolution d’un problème permettant de décrire les étapes vers le résultat. En d’autres termes, un algorithme est une suite finie et non-ambiguë d’instructions permettant de donner la réponse à un problème.

Le programme de seconde a été conçu pour être enseigné et mis en œuvre en s’appuyant assez largement sur les progrès de la science et de la technique informatique,
qu’il s’agisse de logiciels ou de la pensée algorithmique.
Depuis une dizaine d’années le développement de l’usage de logiciels (calculatrice ou ordinateur) a permis de développer chez les élèves la capacité d’expérimenter.
C’est dans ce contexte que l’introduction d’une familiarisation avec l’algorithmique prend sa place dans une pratique des mathématiques.

Algorithmes non mathématiques :
Même si les algorithmes sont souvent considérés comme étant du ressort exclusif des mathématiques et de l’informatique, leur champ d’application est en réalité beaucoup plus vaste.
Un algorithme, très simplement, c’est une méthode.
C’est une façon systématique de procéder pour faire quelque chose :
trier des objets, situer des villes sur une carte, multiplier deux nombres, extraire une racine carrée, chercher un mot dans le dictionnaire…
En tant que méthode, il répond donc à des questions du type :
« comment faire ceci ? », « obtenir cela ? », « trouver telle information ? », . . .
C’est un concept pratique, qui traduit la notion intuitive de procédé systématique,  applicable mécaniquement, sans réfléchir, en suivant simplement un mode d’emploi  précis.
Exemple :
Une recette de cuisine est un algorithme.
Elle en contient les éléments constitutifs :
des entrées (les ingrédients, le matériel utilisé)
des instructions élémentaires simples,
dont l’exécution amène au résultat voulu
un résultat : le plat préparé.
Cependant, les recettes de cuisine ne sont en général pas présentées rigoureusement sous forme non ambiguë : il est d’usage d’y employer des termes vagues laissant une liberté d’appréciation à l’exécutant alors qu’un algorithme stricto sensu doit être précis et sans ambiguïté.
Le tissage surtout tel qu’il a été automatisé par le métier Jacquard est une activité  algorithmique.
Un casse-tête, tel le Rubik’s Cube, peut être résolu de façon systématique par un  algorithme d’exécution.
En sport, l’exécution de séquences répondant à des finalités d’attaque, de défense, de  progression, correspond à des algorithmes.

Source :
http://fr.wikipedia.org/wiki/Algorithmique
http://media.eduscol.education.fr/file/Programmes/17/8/Doc_ress_algo_v25_109178.pdf
https://interstices.info/jcms/c_5776/quest-ce-quun-algorithme
http://fr.wikipedia.org/wiki/Algorithme